Over the previous few weeks, I have developed an interest in physics simulations. I will attempt to create my own in gravity simulation in Python/Pygame. The completed code can be found here:
https://github.com/ggrainger34/pygameGravityEngine
The Laws of Gravity
The goal of this task is to simulate Newton’s Law of Universal Gravitation for an arbitrary number of bodies in a 2 dimensional plane. Each body can each vary by mass, position and velocity. The equation required to calculate the force (and therefore position) between two bodies are as such:
F = G\frac{m_1m_2}{r^2}Where r is the distance between bodies, m1 is the mass of body that the force is acting upon and m2 is the mass of second body and G is the universal Gravitational Constant (https://en.wikipedia.org/wiki/Gravitational_constant).
This equation gives us the force that a body will experience when acted on by another body. This will be useful later.
Creating the interface
For this project, I will be using pygame with python display and calculate the movement of the bodies.
We will create a body class so that new bodies can be created. We will give it different properties including, its position, velocity, radius and mass.
#bodyList is an array of all bodies affected by the gravitational force
bodyList = []
#Define class body
class Body:
def __init__(self, posX, posY, velX, velY, mass, bodyRadius, image):
#Load the sprite image
bodyImage = pygame.image.load(image)
#Define mass, x and y postions and x and y velocities
#Velocities will be used to update the position of the body
self.posX = posX
self.posY = posY
self.velX = velX
self.velY = velY
self.mass = mass
self.bodyRadius = bodyRadius
#Body centre, from where all calculations are carried out
self.bodyCentreX = self.posX + (self.bodyRadius / 2)
self.bodyCentreY = self.posY + (self.bodyRadius / 2)
#The list of previousLocations is used to render the trail of the body
self.previousLocations = []
#Scale the body according to the given size of the body
self.bodyImage = pygame.transform.scale(bodyImage, (self.bodyRadius, self.bodyRadius))
#Add the new body to the body list - this is used in calculations
bodyList.append(self)We will also create a new list called bodyList and whenever a new body is created, it is appended to the body list. This will be used to calculate the forces acting on the body.
Outside of any classes, we will create our ‘main’ function. This is where the program starts:
def makeNewBody():
mousePos = pygame.mouse.get_pos()
Body(mousePos[0],mousePos[1], 0, 0, 400, 30, 'Object.png')
#Initialise the pygame screen and set dimensions, clock speed and title of application
pygame.init()
screen = pygame.display.set_mode(screenSize)
pygame.display.set_caption('n-body Simulation')
clock = pygame.time.Clock()
#Keep running the simulation until the user decides to quit
mouseDownLastFrame = False
prevCounter = perf_counter()
currentTime = perf_counter()
while True:
currentMouse = False
for event in pygame.event.get():
if event.type == pygame.QUIT:
pygame.quit()
exit()
elif event.type == pygame.MOUSEBUTTONDOWN:
currentMouse = True
if currentMouse and not mouseDownLastFrame:
makeNewBody()
if (currentTime - prevCounter) > eulerTimeStep:
#Clear screen
screen.fill((0,0,0))
#Update screen
pygame.display.update()
prevCounter = perf_counter()
currentTime = perf_counter()
mouseDownLastFrame = currentMouseThe function makeNewBody() handles the creation of new bodies so that when the user click on the window, a new body is created in that location. The simulation now looks like this:
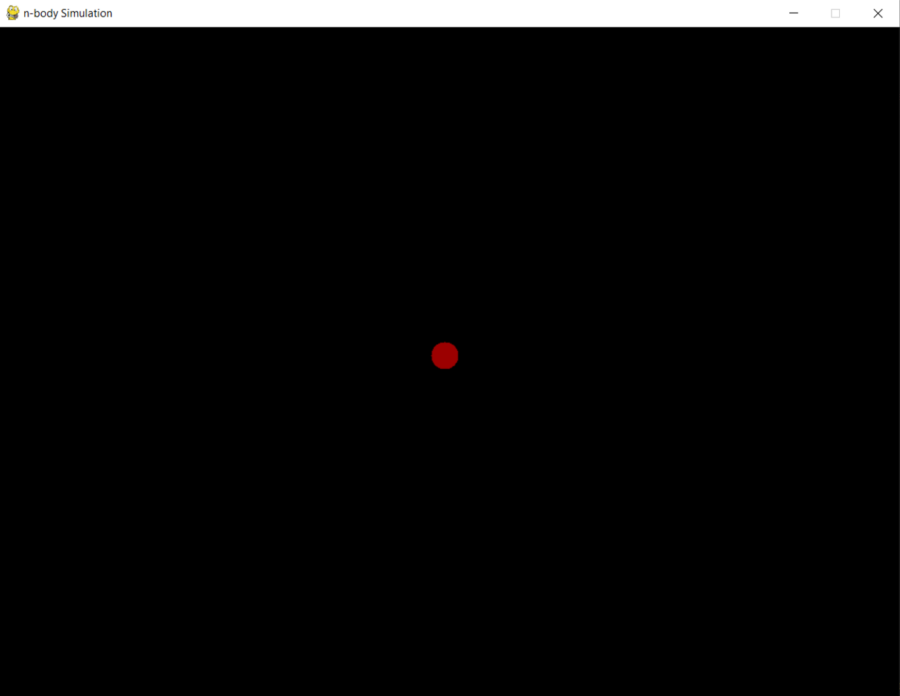
New bodies can be created when a user clicks on the screen.
Normalising and Resolving Forces
We will split the force into a vector with respect to the unit vectors x and y. We will do this by calculating a unit vector in the direction of the other body and multiplying by the magnitude of the force, in this case F. We will then put the resolved direction into a new vector called F.
As we are creating an n body simulation, there will be multiple forces acting on the body, so we need to calculate the resultant force (i.e the overall force). This can be given by summing together all forces acting on the body. For the purposes of the simulation we will count positive direction as to the right and positive direction as upwards.
\vec{F}_{res} = \sum\limits_{n=1}^N{\vec{F}_n}Where N is the number of bodies acting on the current body.
From this the acceleration can be calculated through newton’s second law:
\vec{F}_{res}=m\vec{a}Therefore:
\vec{\ddot{x}}=\frac{\vec{F}_{res}}{m}This differential equation cannot be solved for more than two bodies, what we have here is an n body problem. However, it can be approximated using numerical integration techniques. In this case, I will be using Euler’s method to approximate the expected position.
Euler’s method works by calculating in ‘time steps’. So that every ‘time step’, we recalculate our acceleration and apply it to our velocity:
v_{n+1}=v_n+hf(t_n, v_n)Where f(tn, vn) is our calculated acceleration (from the previous section) and h is the ‘time step’.
Using this method, we can somewhat accurately predict the movement of bodies without having to perform any integration.
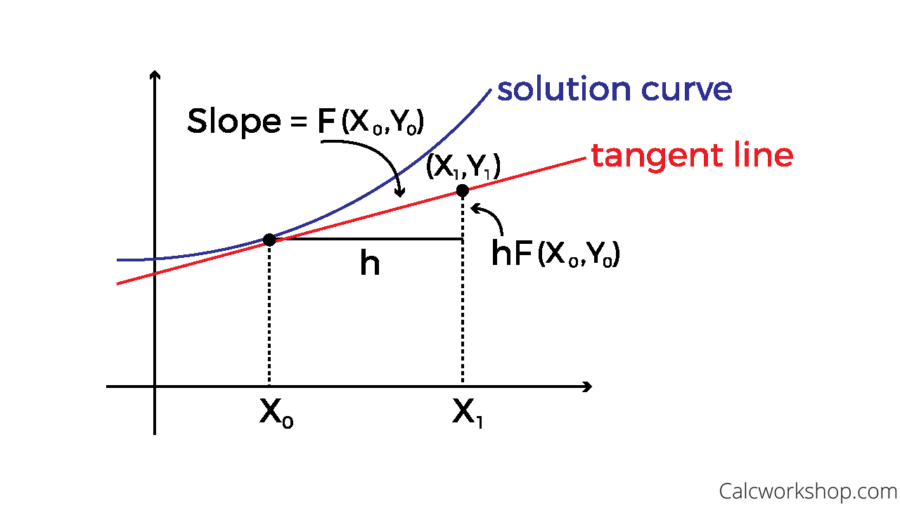
For example, let’s suppose that the acceleration, a is always 9.8m/s2, and the initial velocity, v is 0m/s, time step h is 0.1 and t0 is 0s. We can estimate the velocity at t=0.2s by applying Euler’s method:
v_1=v_0+hf(t_0, v_0) = 0.98m/s
v_2 = v_1 + hf(t_1,v_1) = 0.98+(0.1)(9.8)=1.96m/s
Now even if the acceleration is constantly changing, this method still works for estimating the velocity of an object.
The more detailed explanation and diagram can be found here.
Implementing Euler’s method
We will now add an update method. So that bodies actually move around. The update method is called every time step.
def update(self):
#Loop through all bodies in the list and calculate how their masses impact the movement of the body
for otherBody in bodyList:
resultantForceX = 0
resultantForceY = 0
singleForceX = 0
singleForceY = 0
#The if statement stops bodies from being attracted to themselves
#If the bodies positions are the same do not count gravitational attraction. As this stops bodies from being attracted to themselves
if not (otherBody.posY == self.posY and otherBody.posX == self.posX):
#The distance between the bodies squared
rSquared = ((otherBody.posX - self.posX) ** 2) + ((otherBody.posY - self.posY) ** 2)
#Find the direction in which the force is acting and normalise both x and y
forceDirectionX = (otherBody.posX - self.posX) / sqrt(rSquared)
forceDirectionY = (otherBody.posY - self.posY) / sqrt(rSquared)
#Newton's law of universal gravitation
singleForceMagnitude = gravitationalConstant * otherBody.mass / rSquared
singleForceX = singleForceMagnitude * forceDirectionX
singleForceY = singleForceMagnitude * forceDirectionY
#Add the forces resulting from all seperate bodies to the resultant force
resultantForceX += singleForceX
resultantForceY += singleForceY
#As F=m_1a and F=G*m_1*m_2 / r^2. We can cut m_1 from the equation. Hence F=a
accelerationX = resultantForceX * eulerTimeStep
accelerationY = resultantForceY * eulerTimeStep
#Update position and velocity after calculating acceleration
self.updateVelocity(accelerationX, accelerationY)
self.updatePosition()
#Update the screen
self.renderTrail()
self.renderBody()
#Add previous locations, this is used for creating a trail
self.previousLocations.append((self.posX + (self.bodyRadius / 2), self.posY + (self.bodyRadius / 2)))
#This code displays where the body has been in all past positions
def renderTrail(self):
for location in self.previousLocations:
pygame.draw.circle(screen, (55,55,55), location, 1)
def renderBody(self):
screen.blit(self.bodyImage, (self.posX, self.posY))
def updateVelocity(self, accelerationX, accelerationY):
self.velX += accelerationX
self.velY += accelerationY
def updatePosition(self):
self.posX += self.velX
self.posY += self.velYI also added a function call to the ‘while True’ loop, so that every time step, the update method is called on every body:
#Calculate the new positions of the bodies
for body in bodyList:
body.update()The simulation currently looks like this:

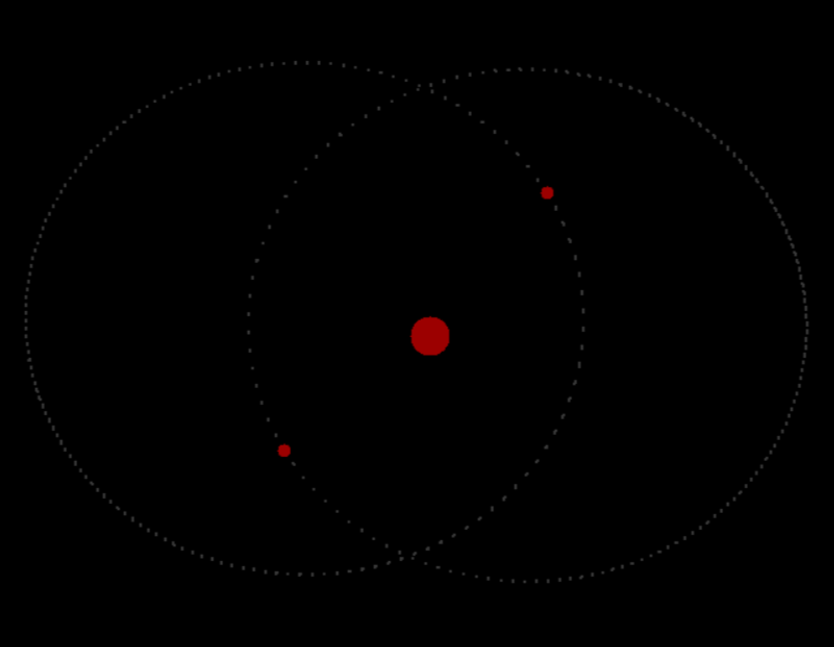
I also added a trail feature, so that it is easy to see where the bodies have previously been. I want to try creating a stable orbit. So I spent some time messing around with different bodies:
Body(500, 500, 0, 0, 30000, 30, 'Object.png')
Body(200, 500, 0, 2, 10, 10, 'Object.png')
Body(800, 500, 0, -2, 10, 10, 'Object.png')Using these initial conditions, its possible to create a semi stable system as shown below:
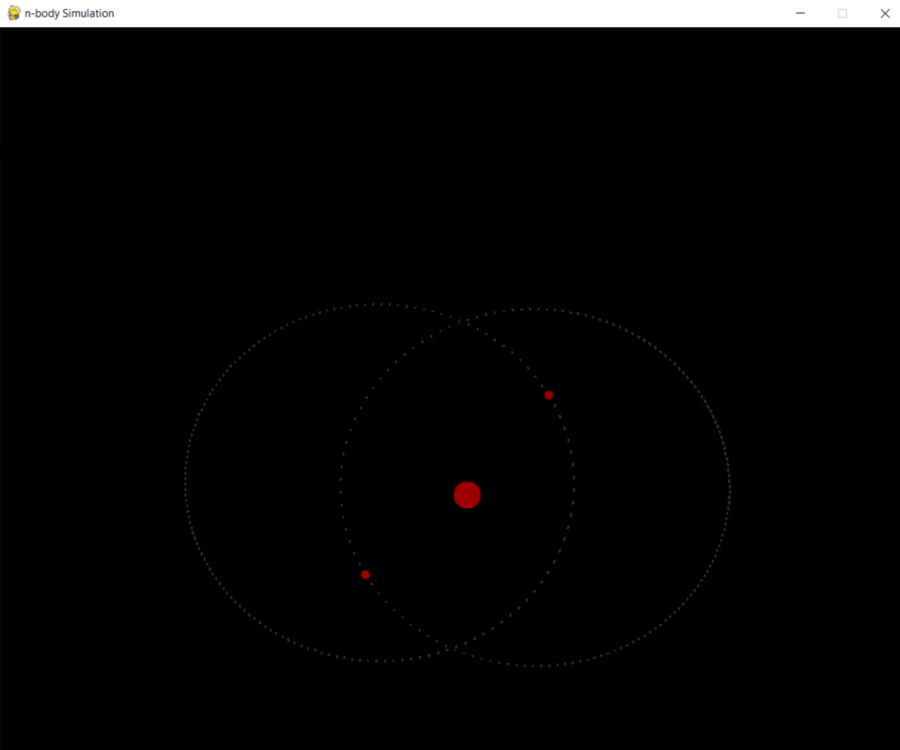
The bodies can now be added and all follow Newton’s Law of Universal Gravitation:
- Improved UI
- Different colours for bodies
- Different coloured trails depending on how long ago the body was there